The Hidden Symmetry of Inverse Sine and Cosine
Mathematics often rewards patient observers with patterns that seemed invisible at first glance. One of my favorite examples links two functions that appear to live on separate islands: the inverse sine and inverse cosine. Ask each function the same question— “what angle corresponds to this ratio?”—and they respond with complementary stories that add up to a single elegant punchline:
\[\cos^{-1}(x) + \sin^{-1}(x) = \frac{\pi}{2}, \quad x \in [-1, 1].\]That equality looks tidy enough to be a textbook trivia fact. Look closer and it becomes a bridge between algebra, geometry, and applied problem solving. Here’s how the symmetry reveals itself and why engineers quietly rely on it.
1. Where the Symmetry Comes From
Algebraic reasoning
Take $\theta = \sin^{-1}(x)$. By definition this means
\[\sin \theta = x, \quad \theta \in \left[-\tfrac{\pi}{2}, \tfrac{\pi}{2}\right].\]Consider the complementary angle $\tfrac{\pi}{2} - \theta$. Its cosine is
\[\cos\!\left(\tfrac{\pi}{2} - \theta\right) = \sin \theta = x.\]So $\tfrac{\pi}{2} - \theta$ is an angle whose cosine equals $x$. By definition that angle is $\cos^{-1}(x)$. Rewriting gives
\[\cos^{-1}(x) = \tfrac{\pi}{2} - \sin^{-1}(x),\]and therefore $\cos^{-1}(x) + \sin^{-1}(x) = \tfrac{\pi}{2}$.
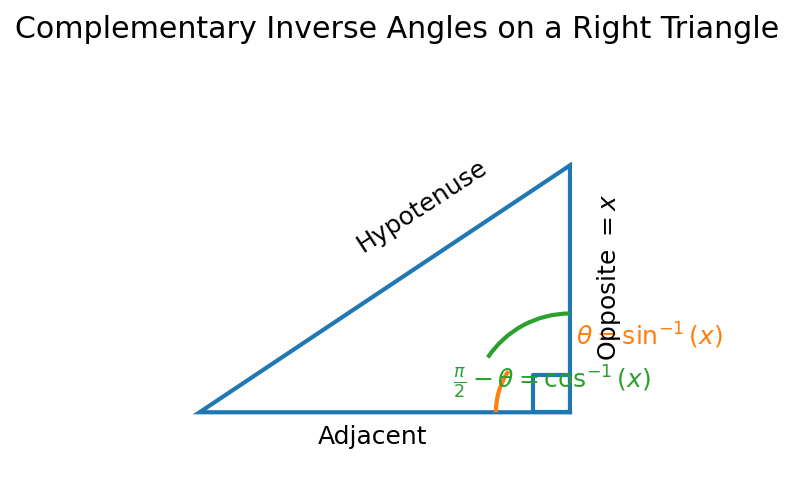
Geometric reasoning
If algebra feels abstract, sketch a right triangle instead. Let one acute angle be $\theta$ with opposite side proportion $x$. The other acute angle must be $\tfrac{\pi}{2} - \theta$. The first angle measures $\sin^{-1}(x)$; the second measures $\cos^{-1}(x)$. Add them together and you hit $\tfrac{\pi}{2}$. Geometry mirrors the algebra perfectly.
2. Turning the Identity into a Tool
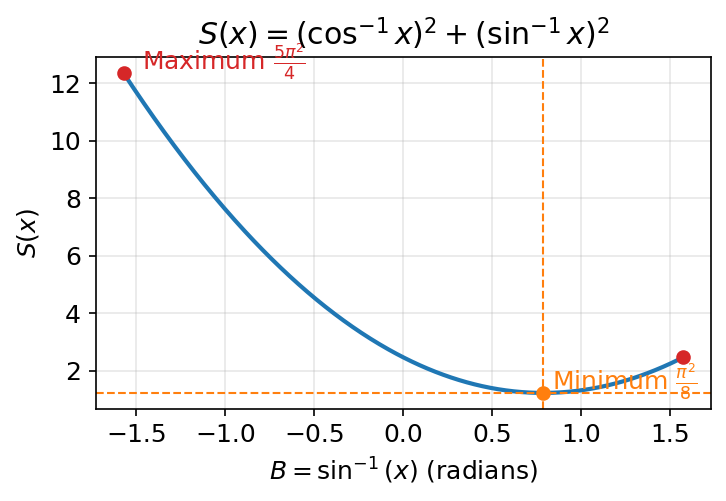
The relationship shines whenever an expression mixes both inverse functions. Consider the function
\[S(x) = (\cos^{-1} x)^2 + (\sin^{-1} x)^2, \quad x \in [-1, 1].\]The squares look intimidating until you substitute the symmetry. Let $B = \sin^{-1}(x)$. Then $\cos^{-1}(x) = \tfrac{\pi}{2} - B$, and
\[S(B) = \left(\tfrac{\pi}{2} - B\right)^2 + B^2 = \tfrac{\pi^2}{4} - \pi B + 2B^2.\]Now it is just a quadratic in $B$ with $B \in [-\tfrac{\pi}{2}, \tfrac{\pi}{2}]$.
- The vertex sits at $B = \tfrac{\pi}{4}$, giving the minimum value $S_{\min} = 2\left(\tfrac{\pi}{4}\right)^2 = \tfrac{\pi^2}{8}$.
- Checking the endpoints reveals $S_{\max} = \tfrac{5\pi^2}{4}$ at $B = -\tfrac{\pi}{2}$.
With almost no calculus, we learn that $S(x)$ ranges from $\tfrac{\pi^2}{8}$ to $\tfrac{5\pi^2}{4}$, a tidy ratio of ten between the extremes.
3. Why Practitioners Care
The arcsine–arccosine partnership shows up any time a physical system needs complementary angles.
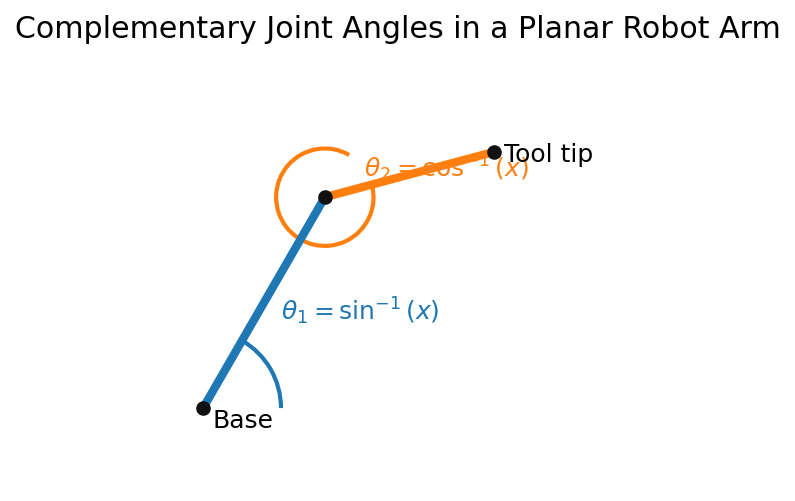
- Robotics kinematics. Solving inverse kinematics for a planar robotic arm produces paired joint angles. The symmetry ensures
that if one joint is computed via $\sin^{-1}$, the neighboring joint can be obtained instantly without another expensive
trigonometric call.
- Signal processing. Decomposing a signal into in-phase and quadrature components often yields angles retrieved via inverse sine and cosine. Their squared sum resembles a phase energy metric, and the identity keeps the algebra compact.
- Structural analysis. Stress directions inside a beam or plate are frequently parameterized with inverse trig expressions. The complementary relationship bounds the angular sweep and helps engineers design for the worst-case loads.
In short: what begins as a classroom curiosity becomes a practical shortcut for keeping calculations stable and predictable.
4. Takeaway
The inverse sine and cosine may look like separate tools, but they answer the same geometric question from different perspectives. Remembering their complementary relationship
\[\cos^{-1}(x) + \sin^{-1}(x) = \tfrac{\pi}{2}\]turns messy expressions into manageable ones and keeps applied math workflows grounded in geometry. The next time an equation throws both functions at you, look for the hidden symmetry first—you might find the entire solution waiting on the other side.