Why Intersection Fails in Lagrange Multipliers: The Geometry of Optimization
Why Intersection Fails in Lagrange Multipliers: The Geometry of Optimization
When learning Lagrange multipliers, students often wonder: why do we need gradients to be parallel? Why can’t we just find where the constraint curve intersects with level sets of our objective function?
The answer reveals a beautiful geometric truth: intersection is about crossing through, while optimization is about touching without crossing.
The Core Insight
Consider optimizing $f(x,y) = x^2 + y^2$ subject to $g(x,y) = x + y - 2 = 0$.
At any point on the constraint line, we can ask: “If I move slightly along the constraint, does $f$ increase or decrease?”
At intersection points: The level curves of $f$ cross the constraint, meaning $f$ has first-order change as we move along the constraint (the function increases or decreases linearly to first approximation).
At tangency points: The level curves touch the constraint without crossing, meaning $f$ has no first-order change as we move along the constraint. The function can still change (usually quadratically), but the first derivative along the constraint is zero.
The Crucial Distinction: First-Order vs Higher-Order Change
You’re absolutely right to question this! At tangency points, $f$ does indeed change as you move along the constraint - but it’s the type of change that matters:
At intersection points:
- Moving distance $\epsilon$ along constraint → $f$ changes by approximately $c_1 \cdot \epsilon$ (linear in $\epsilon$)
- First derivative along constraint ≠ 0
- You can improve by moving further in the same direction
At tangency points (critical points):
- Moving distance $\epsilon$ along constraint → $f$ changes by approximately $c_2 \cdot \epsilon^2$ (quadratic in $\epsilon$)
- First derivative along constraint = 0 (this is the Lagrange condition!)
- Second derivative determines if it’s a maximum (negative) or minimum (positive)
- You can’t improve by moving in either direction (to first order)
Mathematical insight: We’re looking for points where $\frac{df}{dt} = 0$ when $t$ parametrizes motion along the constraint, not where $f$ is constant.
What Do We Mean by “First-Order Change”?
When we move a short distance $\epsilon$ along a curve, the Taylor expansion of $f$ around the starting point looks like:
\[f(\epsilon) = f(0) + c_1\epsilon + c_2\epsilon^2 + c_3\epsilon^3 + \cdots\]The first-order change is captured by the linear term $c_1\epsilon$. If $c_1 \neq 0$, the change in $f$ is primarily linear for small steps. If $c_1 = 0$, the first non-zero term comes from $c_2\epsilon^2$, so the leading change is quadratic.
Two One-Dimensional Examples
- Non-critical point — $f(x) = x^2 + 3x + 5$ at $x=0$:
- $f’(0) = 3$, $f’‘(0) = 2$.
- Move by $\epsilon = 0.1$: true change $\approx 0.31$. The linear term $3\epsilon = 0.30$ already captures almost the whole change. The second-order contribution adds the remaining $0.01$.
- Critical point — $f(x) = x^2 + 5$ at $x=0$:
- $f’(0) = 0$, $f’‘(0) = 2$.
- Move by $\epsilon = 0.1$: the linear term vanishes, and the change is dominated by the quadratic term $\frac{1}{2}f’‘(0)\epsilon^2 = 0.01$.
The second example mirrors what happens at a constrained optimum: once the linear (first-order) variation is eliminated, you only see second-order effects.
First-Order Change: Unconstrained vs Constrained
The phrase “first-order change” depends on the directions you are allowed to move.
- Unconstrained: you can move in any direction, so the gradient must vanish completely. Critical points satisfy $\nabla f = \mathbf{0}$.
- Constrained: you may only move along directions tangent to the constraint. The requirement is $\frac{df}{dt} = \nabla f \cdot \mathbf{T} = 0$ for every tangent direction $\mathbf{T}$. The gradient itself need not vanish; it just cannot have a component along the tangent. This is precisely the Lagrange condition $\nabla f = \lambda \nabla g$.
Parametrising the constraint as $(x(t), y(t))$ confirms the picture:
\[\frac{df}{dt} = \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt} = \nabla f \cdot \mathbf{T},\]and because $\nabla g$ is perpendicular to $\mathbf{T}$, the parallel-gradient condition makes $\frac{df}{dt}$ vanish. So the “first-order change” along the feasible directions really is zero at the constrained optimum, even though individual partial derivatives remain non-zero.
Mathematical Foundation: Why Gradients Must Be Parallel
The Constraint Defines a Path
When we have constraint $g(x,y) = c$, we’re restricted to move along this curve. The tangent vector to this curve at any point $(x_0, y_0)$ is perpendicular to $\nabla g(x_0, y_0)$.
The Objective Function Has a Direction of Steepest Ascent
The gradient $\nabla f(x_0, y_0)$ points in the direction of steepest increase of $f$.
The Parallel Condition Ensures No First-Order Change
If $\nabla f$ and $\nabla g$ are not parallel, then $\nabla f$ has a component tangent to the constraint curve. This means:
- Moving along the constraint will change $f$ linearly (first-order change)
- $\frac{df}{dt} \neq 0$ along the constraint curve
- We’re not at an extremum - we can improve by moving further
If $\nabla f$ and $\nabla g$ are parallel, then $\nabla f$ is perpendicular to the constraint curve:
- $\frac{df}{dt} = 0$ along the constraint (no first-order change)
- $f$ may still change quadratically (second-order), determining max/min
- We’ve found a critical point - a candidate for an extremum
Key insight: The condition $\nabla f = \lambda \nabla g$ ensures the first derivative of $f$ along the constraint is zero, not that $f$ is constant along the constraint.
Example 1: The Intersection That Fails
Problem: Minimize $f(x,y) = x^2 + y^2$ subject to $g(x,y) = x + y - 4 = 0$.
The Wrong Approach: Looking for Intersections
Let’s see what happens if we find where level curves intersect the constraint:
Level curve $f(x,y) = 8$ intersects $x + y = 4$ when: \(x^2 + y^2 = 8 \quad \text{and} \quad x + y = 4\)
Solving: $y = 4 - x$, so $x^2 + (4-x)^2 = 8$ \(x^2 + 16 - 8x + x^2 = 8\) \(2x^2 - 8x + 8 = 0\) \(x^2 - 4x + 4 = 0\) \((x-2)^2 = 0\)
This gives $x = 2, y = 2$, so the intersection point is $(2,2)$.
Why This Point Fails as an Extremum
At $(2,2)$:
- $\nabla f(2,2) = (4, 4)$
- $\nabla g(2,2) = (1, 1)$
- $\nabla f = 4 \nabla g$ ✓
Wait—this actually is the correct answer! But let’s see what happens with a different level curve.
A Better Example of Intersection Failure
Consider level curve $f(x,y) = 5$: \(x^2 + y^2 = 5 \quad \text{and} \quad x + y = 4\)
From $y = 4 - x$: $x^2 + (4-x)^2 = 5$ \(x^2 + 16 - 8x + x^2 = 5\) \(2x^2 - 8x + 11 = 0\)
The discriminant is $64 - 88 = -24 < 0$, so no real intersection exists.
This shows us something important: level curves don’t randomly intersect the constraint—intersection points have special properties that we need to examine carefully.
Example 2: A Clear Intersection vs Tangency Case
Problem: Minimize $f(x,y) = xy$ subject to $g(x,y) = x^2 + y^2 - 1 = 0$ (unit circle).
Step 1: Find the Critical Points (Lagrange Method)
\(\nabla f = \lambda \nabla g\) \((y, x) = \lambda (2x, 2y)\)
This gives us:
- $y = 2\lambda x$ … (1)
- $x = 2\lambda y$ … (2)
- $x^2 + y^2 = 1$ … (3)
From (1) and (2): $y = 2\lambda x$ and $x = 2\lambda y$ \(y = 2\lambda x = 2\lambda(2\lambda y) = 4\lambda^2 y\)
If $y \neq 0$: $1 = 4\lambda^2$, so $\lambda = \pm\frac{1}{2}$
Case 1: $\lambda = \frac{1}{2}$
- $y = x$, and from $x^2 + y^2 = 1$: $2x^2 = 1$
- Critical points: $(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$ and $(-\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}})$
Case 2: $\lambda = -\frac{1}{2}$
- $y = -x$, and from $x^2 + y^2 = 1$: $2x^2 = 1$
- Critical points: $(\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}})$ and $(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$
Step 2: Analyze Intersection vs Tangency
At the critical point $(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$:
- $f = \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} = \frac{1}{2}$
- The level curve $f(x,y) = \frac{1}{2}$ (hyperbola $xy = \frac{1}{2}$) is tangent to the unit circle
At a non-critical point like $(1,0)$:
- $f = 1 \cdot 0 = 0$
- The level curve $f(x,y) = 0$ (the axes $x = 0$ or $y = 0$) intersects the circle
- Since $\nabla f(1,0) = (0,1)$ and $\nabla g(1,0) = (2,0)$ are not parallel, this isn’t optimal
Neighborhood Analysis: The Walking Test
Here’s the intuitive “walking test” for understanding why intersection fails and tangency succeeds:
Walking Near an Intersection Point
Imagine walking along the constraint curve near a point where it intersects (but isn’t tangent to) a level curve of $f$.
What happens: As you walk along the constraint, you cross level curves of $f$. This means $f(x,y)$ is either increasing or decreasing as you move. You’re not at an optimum—you can do better by continuing to walk!
Walking Near a Tangency Point
Now imagine walking along the constraint curve near a tangency point.
What happens: The level curve of $f$ just touches the constraint without crossing. As you walk along the constraint:
- To first order, $f$ doesn’t change (you stay on the same level curve)
- To second order, $f$ either increases on both sides (local minimum) or decreases on both sides (local maximum)
- You’ve found an extremum!
Concrete Neighborhood Calculation
Let’s verify this with our circle example at the critical point $(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$.
Parametrize the constraint: $x = \cos t, y = \sin t$ Objective along constraint: $h(t) = xy = \cos t \sin t = \frac{1}{2}\sin(2t)$
At $t = \frac{\pi}{4}$ (our critical point):
- $h’(\frac{\pi}{4}) = \cos(\frac{\pi}{2}) = 0$ ✓ (First derivative is zero)
- $h’’(\frac{\pi}{4}) = -2\sin(\frac{\pi}{2}) = -2 < 0$ (Local maximum)
Walking test:
- At $t = \frac{\pi}{4} - \epsilon$: $h(t) = \frac{1}{2}\sin(\frac{\pi}{2} - 2\epsilon) \approx \frac{1}{2}(1 - 2\epsilon) = \frac{1}{2} - \epsilon$
- At $t = \frac{\pi}{4} + \epsilon$: $h(t) = \frac{1}{2}\sin(\frac{\pi}{2} + 2\epsilon) \approx \frac{1}{2}(1 + 2\epsilon) = \frac{1}{2} + \epsilon$
Wait, this shows the function increasing on one side! Let me recalculate:
Actually, $h(t) = \frac{1}{2}\sin(2t)$, so:
- $h’(t) = \cos(2t)$
- $h’‘(t) = -2\sin(2t)$
At $t = \frac{\pi}{4}$:
- $h’(\frac{\pi}{4}) = \cos(\frac{\pi}{2}) = 0$ ✓
- $h’’(\frac{\pi}{4}) = -2\sin(\frac{\pi}{2}) = -2 < 0$ ✓ (Local maximum)
For small $\epsilon$: \(h(\frac{\pi}{4} \pm \epsilon) \approx h(\frac{\pi}{4}) + h''(\frac{\pi}{4})\frac{\epsilon^2}{2} = \frac{1}{2} - \epsilon^2\)
So moving in either direction from the critical point decreases the function—confirming it’s a local maximum!
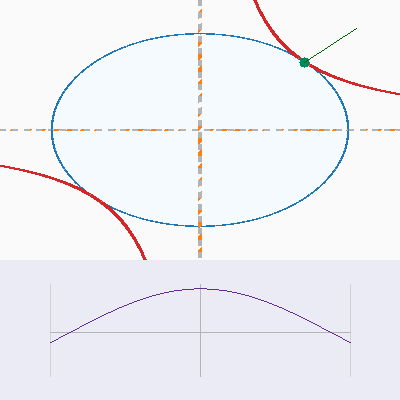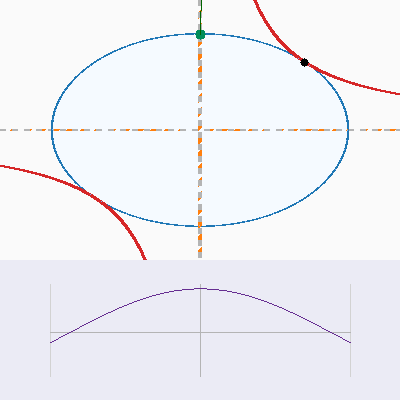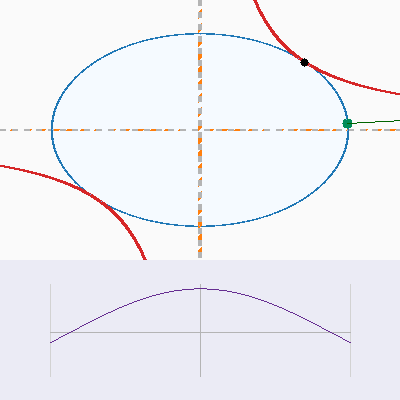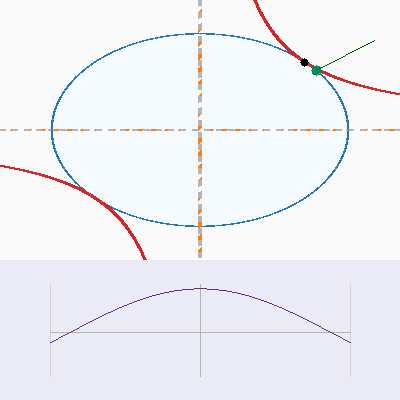
Interactive geometry
The first pair of panels shows the saddle surface $f(x,y) = xy$ together with the unit-circle constraint. Rotate and zoom to watch how the constraint curve threads through the surface, and note how the gradient arrows either disagree (intersection) or align (tangency).
Constraint plane view
The top-down plots strip away the height, leaving the constraint curve and level sets. Compare how the gradients behave directly on the $xy$-plane.
Example 3: The Deceptive Intersection
Problem: Maximize $f(x,y) = x + 2y$ subject to $x^2 + y^2 = 5$.
The Intersection Approach (Wrong)
Let’s find where the line $x + 2y = k$ intersects the circle $x^2 + y^2 = 5$ for various values of $k$.
From the line: $x = k - 2y$ Substituting: $(k - 2y)^2 + y^2 = 5$ \(k^2 - 4ky + 4y^2 + y^2 = 5\) \(5y^2 - 4ky + (k^2 - 5) = 0\)
For intersections to exist: $\Delta = 16k^2 - 20(k^2 - 5) \geq 0$ \(16k^2 - 20k^2 + 100 \geq 0\) \(100 - 4k^2 \geq 0\) \(k^2 \leq 25\) \(-5 \leq k \leq 5\)
Key observation: The lines $x + 2y = 5$ and $x + 2y = -5$ are tangent to the circle, while $x + 2y = k$ for $-5 < k < 5$ intersect the circle at two points.
The Lagrange Approach (Correct)
\(\nabla f = \lambda \nabla g\) \((1, 2) = \lambda (2x, 2y)\)
This gives:
- $1 = 2\lambda x \Rightarrow x = \frac{1}{2\lambda}$
- $2 = 2\lambda y \Rightarrow y = \frac{1}{\lambda}$
- $x^2 + y^2 = 5$
Substituting: $\frac{1}{4\lambda^2} + \frac{1}{\lambda^2} = 5$ \(\frac{5}{4\lambda^2} = 5\) \(\lambda^2 = \frac{1}{4}\) \(\lambda = \pm\frac{1}{2}\)
Case 1: $\lambda = \frac{1}{2}$
- $x = 1, y = 2$
- $f(1,2) = 1 + 4 = 5$ (maximum)
Case 2: $\lambda = -\frac{1}{2}$
- $x = -1, y = -2$
- $f(-1,-2) = -1 - 4 = -5$ (minimum)
Why Intersection Points Fail
Consider the intersection points where $x + 2y = 3$ meets $x^2 + y^2 = 5$.
From our quadratic: $5y^2 - 12y + 4 = 0$ \(y = \frac{12 \pm \sqrt{144 - 80}}{10} = \frac{12 \pm 8}{10}\)
So $y = 2, x = -1$ or $y = 0.4, x = 2.2$.
At $(2.2, 0.4)$:
- $\nabla f = (1, 2)$
- $\nabla g = (4.4, 0.8) = 4.4(1, 0.182)$
These aren’t parallel! The ratio would need to be $\frac{1}{1} = \frac{2}{0.182}$, but $\frac{2}{0.182} \approx 11 \neq 1$.
Neighborhood analysis: Moving along the circle from this intersection point will change the value of $x + 2y$, so it’s not optimal.
The Visual Proof: Gradient Geometry
The most compelling argument comes from visualizing the gradients:
At Intersection Points
- $\nabla f$ (direction of steepest ascent) points in some direction
- $\nabla g$ (perpendicular to constraint) points in another direction
- These directions don’t align
- Consequence: There’s a component of $\nabla f$ tangent to the constraint
- Meaning: Moving along the constraint changes $f$
- Conclusion: Not optimal
At Tangency Points
- $\nabla f$ and $\nabla g$ are parallel: $\nabla f = \lambda \nabla g$
- $\nabla f$ is perpendicular to the constraint curve
- Consequence: No component of $\nabla f$ tangent to the constraint
- Meaning: No first-order change in $f$ when moving along constraint
- Conclusion: Critical point (potential optimum)
A Physics Analogy: Rolling Ball on a Track
Imagine a ball rolling on a frictionless track under gravity, where:
- The track represents your constraint $g(x,y) = c$
- The height represents your objective function $f(x,y)$
- Gravity represents $-\nabla f$ (pointing toward lower values)
At intersection points: Gravity has a component along the track—the ball accelerates and doesn’t stop.
At tangency points: Gravity is perpendicular to the track—the ball has no acceleration along the track and naturally stops (equilibrium).
The Lagrange multiplier method finds these equilibrium points where the “force” (gradient) is perpendicular to the allowed motion (constraint curve).
Advanced Example: The Saddle Point Case
Problem: Find extrema of $f(x,y) = xy$ subject to $x^2 - y^2 = 1$ (hyperbola).
Lagrange Analysis
\(\nabla f = \lambda \nabla g\) \((y, x) = \lambda (2x, -2y)\)
This gives:
- $y = 2\lambda x$ … (1)
- $x = -2\lambda y$ … (2)
- $x^2 - y^2 = 1$ … (3)
From (1) and (2): $x = -2\lambda y = -2\lambda(2\lambda x) = -4\lambda^2 x$
If $x \neq 0$: $1 = -4\lambda^2$, which is impossible since $\lambda^2 \geq 0$.
So we must have $x = 0$ or $y = 0$. But from the constraint $x^2 - y^2 = 1$:
- If $x = 0$: $-y^2 = 1$ (impossible)
- If $y = 0$: $x^2 = 1$, so $x = \pm 1$
Critical points: $(1, 0)$ and $(-1, 0)$ Function values: $f(1,0) = 0$ and $f(-1,0) = 0$
Neighborhood Analysis
Parametrize the hyperbola: $x = \sec t, y = \tan t$
Objective along constraint: $h(t) = \sec t \tan t$
At $t = 0$ (point $(1,0)$):
- $h’(t) = \sec t \tan^2 t + \sec^3 t$
- $h’(0) = 0 + 1 = 1 \neq 0$
This suggests $(1,0)$ is not a critical point! Let me recalculate…
Actually, let me use a simpler parametrization. From $x^2 - y^2 = 1$: For the right branch: $x = \sqrt{1 + y^2}$ \(h(y) = y\sqrt{1 + y^2}\) \(h'(y) = \sqrt{1 + y^2} + \frac{y^2}{\sqrt{1 + y^2}} = \frac{1 + 2y^2}{\sqrt{1 + y^2}}\)
At $y = 0$: $h’(0) = 1 \neq 0$
This confirms that something’s wrong with my calculation. Let me recalculate the Lagrange conditions:
\((y, x) = \lambda (2x, -2y)\)
- $y = 2\lambda x$
- $x = -2\lambda y$
Substituting the first into the second: $x = -2\lambda(2\lambda x) = -4\lambda^2 x$
For this to hold with $x \neq 0$, we need $1 = -4\lambda^2$, which is impossible.
The issue: This hyperbola constraint has no critical points! The function $xy$ has no extrema on the hyperbola $x^2 - y^2 = 1$. As $y \to \pm\infty$ along the constraint, $f(x,y) = xy \to \pm\infty$.
This example shows that not all constrained optimization problems have solutions—another reason why the geometric understanding is crucial.
Summary: The Fundamental Geometric Principle
The key insight of Lagrange multipliers is beautifully geometric:
Intersection = Crossing = Not Optimal
- Level curves cross the constraint
- Function value changes as you move along constraint
- Gradients are not parallel
- You can improve by continuing along the constraint
Tangency = Touching = Potential Optimum
- Level curves touch but don’t cross the constraint
- No first-order change in function along constraint
- Gradients are parallel ($\nabla f = \lambda \nabla g$)
- You’ve found a critical point
This geometric intuition transforms the abstract algebraic condition $\nabla f = \lambda \nabla g$ into a vivid mental picture: we’re looking for points where level curves of the objective function just kiss the constraint curve without crossing it.
The method works because optimization is fundamentally about finding points where you can’t improve by moving—and intersection points are precisely the points where you can still improve by moving!
Further Reading
- Apostol, T.M. - Mathematical Analysis (Chapter on Lagrange multipliers)
- Fleming, W. - Functions of Several Variables (Geometric approach to optimization)
- Simmons, G.F. - Calculus with Analytic Geometry (Intuitive explanations with diagrams)
- Rudin, W. - Principles of Mathematical Analysis (Rigorous treatment of constrained optimization)
The visual understanding developed here forms the foundation for more advanced topics like KKT conditions, penalty methods, and constrained optimization in machine learning.



